"Merely adding arithmetically the proven reserves reported by each of the countries of the world significantly underestimates the true figure. These data instead need to be added probabilistically rather than arithmetically, with the result that the true reserves for the world may be nearly twice the conventional figure."
Dr Richard Pike – formerly a senior manager at BP, and then Chief Executive of the Royal Society of Chemistry - speaking about oil reserves in an interview in 2006[1].How could this vast underestimation of such important information happen? And, why? You may also be wondering what all of this has to do with consumer exposure. It all comes down to working with data, statistics and mathematical models.
The impact of this is that decision makers end up working with poor information when attempting to make important decisions. For example, the environmental challenges which we face could be much greater than currently expected. And knowing the world’s oil reserves is of course not just important in terms of environmental sustainability; the petroleum industry is hugely important in economic terms.
The “why” is not fully clear. The correct models that should be used in these estimates are well known, as is the fact that underestimates are occurring in the industry.
It’s in the best interest of each oil company to know accurately what their own reserves are. Within each company there are analysts who accurately calculate oil reserves using statistically valid approaches; these reserves are typically reported in percentile form. The underestimates occur when attempting to aggregate across organizations – to get national and global estimates.[a]
This is where the link with aggregate consumer exposure is important.

The “how” is much clearer. A summary is provided in the quote by Dr Pike above. And it’s the “how” which is particularly relevant to the general science of risk assessment, and of course, aggregate consumer exposure assessment.
Trusted models exist for the estimation of the smallest amount of oil a single field is likely to produce (called the “provable” reserve – it equates to the 10th percentile of expected oil production) [2]. However, in calculating aggregate reserves from a number of fields (for example all the oil fields in operation by a single company), the estimates for each are sometimes added arithmetically, instead of using statistically valid methods (or expert models). This simplistic calculation tends to greatly underestimate the total reserve, based on the individual estimates. And the situation gets worse when reserves are totalled to get national reserves, and again when calculating global reserves.
A simple example illustrates why the simple addition of these estimates is not correct. Since we are talking probabilities, let’s replace our oil fields with dice. Throw a single dice and you are very likely to get a score of more than 1. In fact there is just a 1/6 = 16% chance you will score just 1. So to use the terminology of statistics and risk analysis – the P16 for expected “return” from the single dice is 1. Now try with 2 dice, and this time let’s try to get a total score of over 4. There are 6 ways you can score 4 or less [4], so the probability of this happening is 6/36 = 16% (again). So, the P16 for expected return from throwing a pair of dice is 4. If we were to have simply added the expected returns from the individual dice, we would have calculated a P16 of 1+1 = 2. It’s quite clear that expected return just doesn’t simply add up in this case – the simple addition suggests a value half of the actual result!
The dice in the above example were assumed fair (without bias towards any particular number), and we assumed also that there was no interdependence between the dice (the scores are independent of each other). However, an interesting thing happens if we ask what would take place if we assume the dice are not independent – but are in fact constructed in some way so that they always scored exactly the same as each other. Now this time, if we were to calculate the probability of scoring a total of 2 or less, the answer would be again 1/6 (as the only possible scores are 2, 4, 6, 8, 10, 12 – and the only way of scoring a 2 or less is to get a pair of 1’s). So then, the P16 for this pair of dice is 2, and the sum of the individual P16s is 1+1 = 2. So the simple summation seems to work perfectly in this situation!
The above is not just a once off example in the case of a pair of magically synchronized dice – the simple summation does in fact yield the correct result when the underlying distributions are perfectly correlated. This is something to bear in mind a little later, but first we can take a quick look at why the summation of percentiles does not usually give the correct result. The problem is of course more general than the estimation of oil reserves, or likely score in a game of dice. The question is one of how we should approach the aggregation of probability distributions. And the answer is often “with great difficulty”. That may seem like the easy answer, but it’s a much more responsible response than to say “let’s just add the values together and see what we get”. Once we acknowledge that we can’t easily find the answer, we’ve started along the right path toward finding it.
Let’s start with the simple (and naive) approach which is to just arithmetically sum the individual P90s of 2 distributions. The situation is depicted visually below, and a little thought brings you to the difficulty of the task at hand. The summation of percentiles is an attempt to determine the statistical properties (for example 90th percentile, P90) of the aggregate probability distribution, using just the corresponding (P90) statistics of the original distributions.
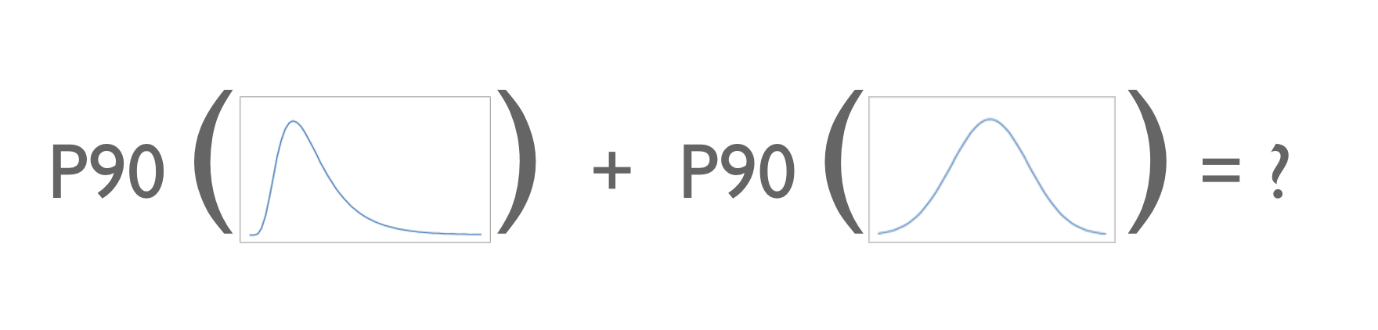 Figure 2. Visual representation of the “equation” for summation of percentiles.
Figure 2. Visual representation of the “equation” for summation of percentiles.
The key problem with the simple approach above is that the P90 values (along with other descriptive statistics) capture just a very tiny amount of information about the full distributions. The P90 alone tells us nothing about the shape of the distribution; the variance, skewness, smoothness, etc.. The aggregate probability distribution itself will naturally depend on the shape of the original distributions, and therefore so too will the P90 of the aggregate distribution.
The correct approach is to leave the calculation of statistics until its needed – so as not to lose the information in the distribution. So what we should really do is “aggregate” the distributions themselves [4]. The mathematically correct method is not to “calculate statistics and then sum them together”, but rather to “add distributions and then calculate statistics”.
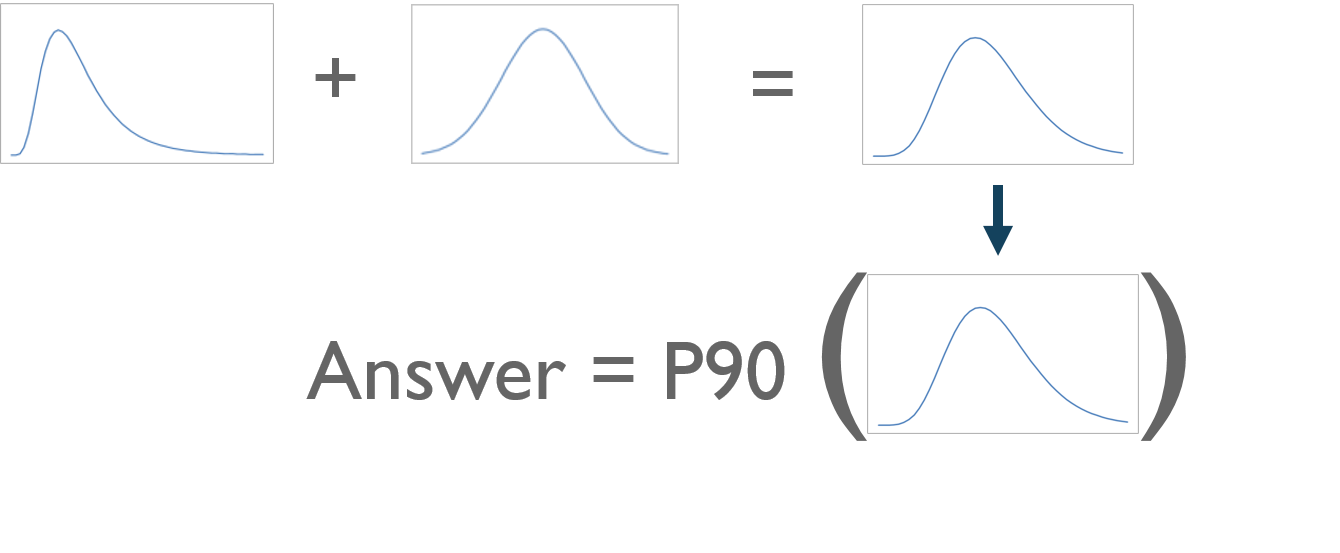 Figure 3. Add distributions and then calculate statistics
Figure 3. Add distributions and then calculate statistics
That is the “how” of the underestimation of oil reserves mentioned earlier. Very simplistic (and frankly, incorrect) mathematical methods are used. The correct method is known, and is shown above. But what can be learned from the point of view of exposure science?
It is very often the case that consumers will be exposed to a particular chemical (additive, flavouring, fragrance, pesticide, etc…) from a number of different sources. As an example, we could consider a flavouring compound which is present in a variety of foods which the general population consumes. In addition, the same compound may be present as a fragrance in the cosmetic products that consumers use on a day-to-day basis. So there are many routes of exposure for this particular chemical. It’s our job as exposure scientists to accurately estimate the likely aggregate exposure from as many routes possible.
We could imagine each consumer holding a collection of dice – one for each possible route of exposure. If we were to assume that we could simply sum the percentiles for each dice (i.e. each route of exposure), we would effectively be assuming that the dice are perfectly correlated (as we showed earlier). And so, if you scored a 6 with one dice, you would score a 6 with all the others.
(A phenomenon which could be useful in a game of Monopoly, but not if we’re talking aggregate consumer exposure!)
This naive summation of percentiles assumes that consumers are exposed at the same relative level from all sources. So the high-end consumers are assumed to have high exposure from all of the sources at the same time. This is a very unrealistic scenario and is effectively saying that the person in the population who eats the most of one food, also eats the most of every other food, as well as being the highest user of each of the cosmetic products which contribute to the exposure. The result is a significant overestimation of the true aggregate exposure, and provides poor information to decision makers.
The truth is that each consumer has much more varied and complex consumption habits, and to calculate the true population aggregate exposure requires effective modelling of these consumption habits – at the individual consumer level. The aggregate exposure distribution can be calculated provided sufficient data is available [5] and the correct models are used.
Unfortunately, this kind of simplistic estimation is still used in numerous areas of risk assessment. It should be clear that the importance of these calculations is very great – as the results are used to shape economic strategy, environmental policies, and to make the regulatory decisions that protect our health and wellbeing.
The majority of exposure scientists will of course know of the limitations of summing exposure percentiles – and most would agree that it is an aspect of our work which we must try to move away from. It’s just not good enough to assume that simple summations are good approximations in this area; the stakes are too high.
Footnotes:
[a] There is also anecdotal evidence of countries underestimating their reserves, to inflate oil prices – which cannot be ruled out as a motivational factor to explain why these underestimates occur. References: Petroleum Review, June 2006, pp. 26, 27.in the oil industry, this is referred to as the P90 – to indicate that there is a 90% probability that the actual yield will be over this value. In consumer exposure, we would refer to this as the “value for which 10% of the population has a lower exposure”, and so we term it the P10.
The 6 combinations are: (1,1), (1,2), (2,1), (2,2), (1,3), (3,1).
Mathematicians might recognize that this equates to a convolution of the distributions.